FETI methods

97. FETI methods#

Finite Element Tearing and Interconnection.

As the name says, we break the global (finite element) system apart, and then reenforce continuity via Lagrange parameters.

from ngsolve import *
from ngsolve.webgui import Draw

from netgen.occ import *
shape = None
mx, my = 3,3
for i in range(mx): 
    for j in range(my):
        rect = MoveTo(i/mx, j/mx).Rectangle(1/mx, 1/my).Face()
        rect.faces.name='mat'+str(i)+str(j)
        shape = Glue([shape,rect]) if shape else rect

shape.edges[Y<1e-4].name = "bot"
mesh = Mesh(OCCGeometry(shape, dim=2).GenerateMesh(maxh=0.04))
print (mesh.GetMaterials())
print (mesh.GetBoundaries())
Draw (mesh);

('mat00', 'mat01', 'mat02', 'mat10', 'mat11', 'mat12', 'mat20', 'mat21', 'mat22')
('bot', 'default', 'default', 'default', 'default', 'default', 'default', 'default', 'default', 'default', 'bot', 'default', 'default', 'default', 'default', 'default', 'default', 'bot', 'default', 'default', 'default', 'default', 'default', 'default')

We define \(H^1\)-spaces on sub-domains \(\Omega_i\). The product spaces is

\[ V = \Pi_i H^1(\Omega_i) \]

fes = None
for dom in mesh.Materials('.*').Split():
    fesi = Compress(H1(mesh, definedon=dom, dirichlet="bot"))
    fes = fes * fesi if fes else fesi

print ("ndof =", fes.ndof)

u, v = fes.TnT()

domtrial = {} 
domtest = {}
for nr,dom in enumerate (mesh.Materials('.*').Split()):
    domtrial[dom] = u[nr]
    domtest[dom] = v[nr]

ndof = 858

We identify the interfaces (i.e. internal boundaries) between two sub-domains. On these \(\gamma_{ij}\) we define spaces for the Lagrange parameter. Although the spaces are \(H^{-1/2}\), we use \(H^1(\gamma_{ij})\) to obtain the same number of constraints as we have basis functions on the interface.

feslam = None
for inter in mesh.Boundaries('.*').Split():
    doms = inter.Neighbours(VOL).Split()
    if len(doms) == 2:
        feslami = Compress(H1(mesh, definedon=inter))
        feslam = feslam * feslami if feslam else feslami 
    
print ("ndof-lam:", feslam.ndof)

lam, mu = feslam.TnT()

intertrial = {} 
intertest = {}
nr = 0
for inter in mesh.Boundaries('.*').Split():
    doms = inter.Neighbours(VOL).Split()
    if len(doms) == 2:
        intertrial[inter] = lam[nr]
        intertest[inter] = mu[nr]
        nr = nr+1

ndof-lam: 108

We define bilinear-forms on the sub-domains:

\[ a(u,v) = \sum_{\Omega_i} \int_{\Omega_i} \nabla u_i \nabla v_i + u_i v_i \]

and the constraint equations

\[ b(u,\mu) = \sum_{\gamma_{ij}} \int_{\gamma_{ij}} (u_i - u_j) \mu_{ij} \]

a = BilinearForm(fes)
f = LinearForm(fes)
b = BilinearForm(trialspace=fes, testspace=feslam)

for (ui,vi) in zip(u,v):
    a += grad(ui)*grad(vi)*dx + 1*ui*vi*dx
    f += y*x*vi*dx
    

for inter in mesh.Boundaries('.*').Split():
    doms = inter.Neighbours(VOL).Split()
    if len(doms) == 2:
        dom1,dom2 = doms
        # a += 1*(domtrial[dom1]-domtrial[dom2])*(domtest[dom1]-domtest[dom2])*ds(inter)
        b += (domtrial[dom1]-domtrial[dom2]) * intertest[inter] * ds(inter)
        
a.Assemble()
b.Assemble()
f.Assemble()

<ngsolve.comp.LinearForm at 0x103b37630>

Obviously, if we only solve the decomposed sub-problems, we don’t get the correct solution:

gfu = GridFunction(fes)
gfu.vec.data = a.mat.Inverse(inverse="sparsecholesky", freedofs=fes.FreeDofs())*f.vec
gftot = CF ( list(gfu.components) )
Draw (gftot, mesh);

Next we solve the saddle-point problem

\[\begin{split} \left( \begin{array}{cc} A & B^T \\ B & 0 \end{array} \right) \left( \begin{array}{c} u \\ \lambda \end{array} \right) = \left( \begin{array}{c} f \\ 0 \end{array} \right) \end{split}\]

We explicitly build the Schur-complement \(S = B A^{-1} B^T\), and use conjugate gradients to solve for the Lagrange parameter \(\lambda\). Then we recover the primal variable \(u\) from the first equation:

ainv = a.mat.Inverse(inverse="sparsecholesky", freedofs=fes.FreeDofs())
S = b.mat @ ainv @ b.mat.T
g = (b.mat @ ainv * f.vec).Evaluate()

from ngsolve.krylovspace import CGSolver
invS = CGSolver(S, pre=IdentityMatrix(feslam.ndof), printrates="\r", maxiter=500)

lam = g.CreateVector()
lam.data = invS * g
gfu.vec.data = ainv * (f.vec - b.mat.T * lam)

CG iteration 1, residual = 0.08403603524990744     
CG iteration 2, residual = 0.03971914630731917     
CG iteration 3, residual = 0.012297034208142892     
CG iteration 4, residual = 0.002090121181283583     
CG iteration 5, residual = 0.001591398613376105     
CG iteration 6, residual = 0.00031727068098377705     
CG iteration 7, residual = 0.0002195604136507497     
CG iteration 8, residual = 0.0006451346034049315     
CG iteration 9, residual = 0.0008052306716672809     
CG iteration 10, residual = 7.795980838199083e-05     
CG iteration 11, residual = 0.00010635661953372284     
CG iteration 12, residual = 4.603458937298973e-05     
CG iteration 13, residual = 4.359929570730049e-05     
CG iteration 14, residual = 5.2523047971054915e-05     
CG iteration 15, residual = 4.790998862263299e-05     
CG iteration 16, residual = 0.00034753181610355826     
CG iteration 17, residual = 4.576539407362843e-05     
CG iteration 18, residual = 5.7142337375036324e-05     
CG iteration 19, residual = 0.00021207948653739032     
CG iteration 20, residual = 3.0652074629359445e-05     
CG iteration 21, residual = 5.11525589850961e-05     
CG iteration 22, residual = 1.4266986447890888e-05     
CG iteration 23, residual = 1.537365841822429e-05     
CG iteration 24, residual = 1.0955599586462566e-05     
CG iteration 25, residual = 1.9015694050720538e-05     
CG iteration 26, residual = 1.1989787406541846e-05     
CG iteration 27, residual = 1.3814027038193696e-05     
CG iteration 28, residual = 8.847652138892995e-06     
CG iteration 29, residual = 2.0924003356633485e-05     
CG iteration 30, residual = 6.7416697520263924e-06     
CG iteration 31, residual = 1.1279478734125653e-05     
CG iteration 32, residual = 3.49700933821718e-06     
CG iteration 33, residual = 1.0832422900323032e-05     
CG iteration 34, residual = 2.43699923936851e-06     
CG iteration 35, residual = 3.981806312827792e-06     
CG iteration 36, residual = 3.2117595881717358e-06     
CG iteration 37, residual = 3.925516231516917e-06     
CG iteration 38, residual = 1.048424197413411e-06     
CG iteration 39, residual = 5.850000589284717e-07     
CG iteration 40, residual = 5.088005797462321e-07     
CG iteration 41, residual = 2.3871960358759823e-06     
CG iteration 42, residual = 5.336922774340354e-07     
CG iteration 43, residual = 4.665423570987992e-07     
CG iteration 44, residual = 6.812732593501901e-07     
CG iteration 45, residual = 6.431605893684529e-07     
CG iteration 46, residual = 6.523698528454081e-07     
CG iteration 47, residual = 1.2196346737945834e-06     
CG iteration 48, residual = 3.3447500609865393e-07     
CG iteration 49, residual = 2.54882003002899e-07     
CG iteration 50, residual = 3.7884609435694837e-07     
CG iteration 51, residual = 2.416328121968302e-07     
CG iteration 52, residual = 7.157521486068638e-07     
CG iteration 53, residual = 3.798445299586633e-07     
CG iteration 54, residual = 2.7442373083841097e-07     
CG iteration 55, residual = 9.458049609855505e-08     
CG iteration 56, residual = 6.804672243371665e-08     
CG iteration 57, residual = 1.442272218649972e-07     
CG iteration 58, residual = 3.442621293290801e-08     
CG iteration 59, residual = 3.091007966741377e-08     
CG iteration 60, residual = 6.27878807852745e-08     
CG iteration 61, residual = 2.3579728561815966e-08     
CG iteration 62, residual = 8.880746884962585e-08     
CG iteration 63, residual = 1.3471576878396266e-08     
CG iteration 64, residual = 5.298751328169241e-08     
CG iteration 65, residual = 3.395765545683244e-08     
CG iteration 66, residual = 2.085600846031722e-08     
CG iteration 67, residual = 2.9638470525464173e-08     
CG iteration 68, residual = 8.928735925956238e-09     
CG iteration 69, residual = 5.553041956306279e-09     
CG iteration 70, residual = 1.287928570758883e-08     
CG iteration 71, residual = 6.6274582953029674e-09     
CG iteration 72, residual = 4.328816366198409e-09     
CG iteration 73, residual = 2.3136123405182263e-08     
CG iteration 74, residual = 8.210994966143734e-09     
CG iteration 75, residual = 9.25520747861709e-09     
CG iteration 76, residual = 3.1379215181523676e-09     
CG iteration 77, residual = 2.3983148456372928e-09     
CG iteration 78, residual = 1.8049787974673716e-09     
CG iteration 79, residual = 2.738448357726513e-09     
CG iteration 80, residual = 9.501326497077893e-10     
CG iteration 81, residual = 1.0442260933347703e-09     
CG iteration 82, residual = 1.1426353562159576e-09     
CG iteration 83, residual = 2.1836326980044262e-09     
CG iteration 84, residual = 1.3708756121207317e-09     
CG iteration 85, residual = 2.8890289283265866e-09     
CG iteration 86, residual = 9.136633102131929e-10     
CG iteration 87, residual = 5.481448176729611e-10     
CG iteration 88, residual = 5.472203194810454e-10     
CG iteration 89, residual = 8.145362214478792e-10     
CG iteration 90, residual = 2.1683248946794615e-10     
CG iteration 91, residual = 2.1212350591307874e-09     
CG iteration 92, residual = 1.3535274317834003e-10     
CG iteration 93, residual = 9.519794840612708e-11     
CG iteration 94, residual = 6.83359210603231e-10     
CG iteration 95, residual = 1.2434410805511616e-10     
CG iteration 96, residual = 6.668030799336058e-11     
CG iteration 97, residual = 2.894042589116169e-10     
CG iteration 98, residual = 7.146891584743952e-11     
CG iteration 99, residual = 2.8812466355847642e-11     
CG iteration 100, residual = 9.622505522919229e-11     
CG iteration 101, residual = 9.336293573816489e-11     
CG iteration 102, residual = 2.25605983613152e-11     
CG iteration 103, residual = 1.472605223362453e-10     
CG iteration 104, residual = 1.3293946721880735e-11     
CG iteration 105, residual = 5.471348358053518e-11     
CG iteration 106, residual = 2.0476606684446096e-11     
CG iteration 107, residual = 8.806585375470873e-12     
CG iteration 108, residual = 6.311445602835678e-12     
CG iteration 109, residual = 4.821283847638357e-12     
CG iteration 110, residual = 7.482820337174943e-12     
CG iteration 111, residual = 3.141193012831149e-11     
CG iteration 112, residual = 4.171407828506235e-12     
CG iteration 113, residual = 7.329662004220288e-12     
CG iteration 114, residual = 3.098908031386727e-12     
CG iteration 115, residual = 1.9544846056068958e-11     
CG iteration 116, residual = 1.6887711955989794e-11     
CG iteration 117, residual = 2.4153430557586915e-12     
CG iteration 118, residual = 7.742092045338669e-12     
CG iteration 119, residual = 1.3932588912478067e-12     
CG iteration 120, residual = 8.07278768037913e-13     
CG iteration 121, residual = 9.65779269426817e-13     
CG iteration 122, residual = 4.875191105188619e-13     
CG iteration 123, residual = 5.671434829595564e-13     
CG iteration 124, residual = 1.3526184819728338e-12     
CG iteration 125, residual = 1.3664780094435506e-12     
CG iteration 126, residual = 1.6229109170864464e-12     
CG iteration 127, residual = 3.1879911736020597e-13     
CG iteration 128, residual = 6.006196822577004e-13     
CG iteration 129, residual = 4.818785985958922e-13     
CG iteration 130, residual = 8.109444401032371e-13     
CG iteration 131, residual = 1.7959723205423837e-12     
CG iteration 132, residual = 5.841797161857024e-13     
CG iteration 133, residual = 3.240426249115194e-13     
CG iteration 134, residual = 1.452604843779021e-13     
CG iteration 135, residual = 1.3756077405841321e-13     
CG iteration 136, residual = 1.2962894036118282e-13     
CG iteration 137, residual = 1.1568776906242914e-13     
CG iteration 138, residual = 2.900927602556945e-14     
CG converged in 138 iterations to residual 2.900927602556945e-14

gftot = CF ( list(gfu.components) )
Draw(gftot, mesh);

97.1. Preconditioner for \(S\)#

The function space for the Lagrange parameter is \(\Pi_{ij} H^{-1/2} (\gamma_{ij})\). The Schur complement matrix scales like a bilinear-form in \(H^{-1/2}\). As a preconditioner, we need a matrix which scales like \(\Pi_{ij} H^{1/2}\). We cheat a bit with the non-additivity of the \(H^{1/2}\)-norm, and use \(\sum_{\Omega_i} \| \operatorname{tr} u \|_{H^{1/2}(\partial \Omega_i)}^2\)

We have to map functions from the skeleton onto the domain:

bnddofs = fes.GetDofs(mesh.Boundaries(".*"))
innerdofs = ~bnddofs

massbnd = BilinearForm(fes)
for (ui,vi) in zip(u,v):
    massbnd += ui*vi*ds
massbnd.Assemble()
invmassbnd = massbnd.mat.Inverse(inverse="sparsecholesky", freedofs=bnddofs)

massinter = BilinearForm(feslam)
for inter in mesh.Boundaries('.*').Split():
    doms = inter.Neighbours(VOL).Split()
    if len(doms) == 2:
        massinter += intertrial[inter]*intertest[inter]*ds(inter)
massinter.Assemble()

emb = invmassbnd@b.mat.T@massinter.mat.Inverse(inverse="sparsecholesky")

used dof inconsistency
(silence this warning by setting BilinearForm(...check_unused=False) )

The \(H^{1/2}(\partial \Omega_i)\)-norms are obtained by forming Schur-complements of the sub-domain matrices with respect to boundary dofs:

SchurDir = a.mat - a.mat@a.mat.Inverse(inverse="sparsecholesky", freedofs=innerdofs)@a.mat

pre = emb.T @ SchurDir @ emb

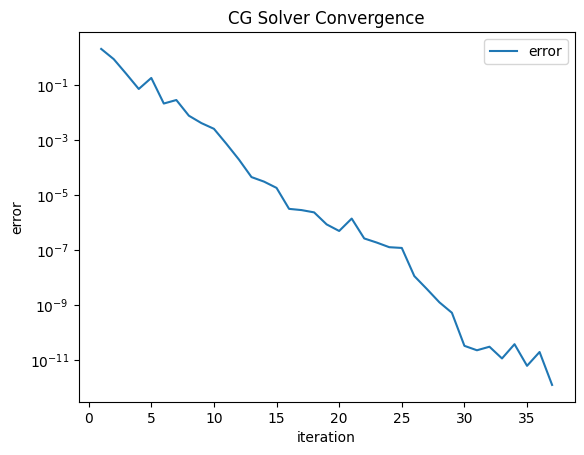
invS = solvers.CGSolver(S, pre=pre, plotrates=True, maxiter=500)

lam = g.CreateVector()
lam.data = invS * g
gfu.vec.data = ainv * (f.vec - b.mat.T * lam)

../_images/d531b85af37cbe80215f74c9ccbffb009e60ec17c75267c108aaeda8de2d1679.png

<Figure size 640x480 with 0 Axes>

Draw(gftot, mesh);

FETI methods

Contents

97. FETI methods#

97.1. Preconditioner for \(S\)#