63. Magnetic flux induced by a coil

We model a current density in a cylindrical coil, and simulate the magnetic field caused by this current.

from ngsolve import *
from netgen.occ import *
from ngsolve.webgui import Draw, FieldLines

coil = Cylinder(Axes((0,0,-0.4),Z), r=0.4, h=0.8) - \
     Cylinder(Axes((0,0,-0.4),Z), r=0.2, h=0.8)
coil.solids.name="coil"
coil.faces.col=(1,0,0)
coil.faces.maxh=0.1

box = Box((-2,-2,-2), (2,2,2) )
box.faces.col=(0,0,1,0.5)
box.faces.name="outer"

air = box-coil
air.solids.name="air"

shape = Glue([coil,air])
Draw (shape);

mesh = Mesh(OCCGeometry(shape).GenerateMesh(maxh=0.5)).Curve(3)
Draw (mesh);

The variational formulation for the magnetic vector-potential is: find \(u \in H(\operatorname{curl})\)

\[ \int \mu^{-1} \operatorname{curl} u \, \operatorname{curl} v \, dx = \int j v \, dx \qquad \forall \, v \]

fes = HCurl(mesh, order=3, dirichlet="outer")
u,v = fes.TnT()

mu = 4*pi*1e-7
a = BilinearForm(1/mu*curl(u)*curl(v)*dx + 1e-6/mu*u*v*dx)
pre = preconditioners.BDDC(a)
a.Assemble()

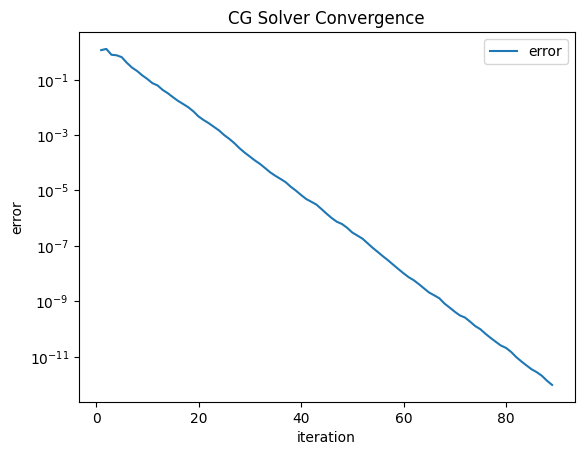
inv = solvers.CGSolver(a.mat, pre.mat, plotrates=True)

tau = CF((y,-x,0))
tau = tau/Norm(tau)

N = 1000 # turns
I = 1  # current
crosssection = 0.2*0.8
j = N*I/crosssection

f = LinearForm(j*tau*v*dx("coil", bonus_intorder=6)).Assemble()

gfu = GridFunction(fes)
gfu.vec.data = inv*f.vec

<Figure size 640x480 with 0 Axes>

ea = { "euler_angles" : (-60, 0, -11) }
clipping = { "clipping" : { "y":1, "z":0, "dist":0.5} }

fieldlines = FieldLines(curl(gfu), mesh.Materials(".*"), length=2, num_lines=100)

Draw(curl(gfu), mesh,  "X", draw_vol=False, draw_surf=True, objects=[fieldlines], \
     min=0, max=5e-4, autoscale=False, settings={"Objects": {"Surface": False, "Wireframe": False}},
    **ea); # , **clipping);