17.2. Implementing the explicit Euler method

We want to implement a time-stepping method for solving the autonomous ODE

\[ y^\prime (t) = f(y(t)) \qquad \forall t \in [0, T], \qquad y(0) = y_0 \]

using the explicit Euler method:

\[ y_{i+1} = y_i + \tau f(y_i) \qquad 0 \leq i < n \]

with \(\tau = T/n\).

Time-stepping methods are implemented in the file timestepper.hpp. The base class looks like

class TimeStepper
{ 
  protected:
    std::shared_ptr<NonlinearFunction> m_rhs;
  public:
    TimeStepper(std::shared_ptr<NonlinearFunction> rhs) : m_rhs(rhs) {}
    virtual ~TimeStepper() = default;
    virtual void doStep(double tau, VectorView<double> y) = 0;
};

It has the right-hand side of the ode as a member (m_rhs), and introduces a virtual function doStep which evolves the state vector y by the time-step tau. It is a pure virtual function, since the base class has no glue how to compute the time-step.

The explicit Euler method is a derived class from TimeStepper:

class ExplicitEuler : public TimeStepper
{
  Vector<> m_vecf;
public:
  ExplicitEuler(std::shared_ptr<NonlinearFunction> rhs) 
  : TimeStepper(rhs), m_vecf(rhs->dimF()) {}
  
  void doStep(double tau, VectorView<double> y) override
  {
    this->m_rhs->evaluate(y, m_vecf);
    y += tau * m_vecf;
  }
};

It implements the update of the state vector by adding \(\tau f(y_n)\) to the vector. It requires one help vector for evaluating \(f\). To avoid reallocation of the vector in every time-step we made it a private class member.

17.2.1. Using the time-stepping method

A mass attached to a spring is described by the ODE

\[ m y^{\prime \prime}(t) = -k y(t), \]

where \(m\) is mass, \(k\) is the stiffness of the spring, and \(y(t)\) is the displacement of the mass. The equation comes from Newton’s law

force = mass \(\times\) acceleration

We replace the second-order equation with a first order system:

\[\begin{eqnarray*} y_0^\prime & = & y_1 \\ y_1^\prime & = & -\frac{k}{m} y_0 \end{eqnarray*}\]

Then we define the right-hand-side as a NonlinearFunction. The derivative is needed for the Newton solver:

class MassSpring : public NonlinearFunction
{
  double m_mass;
  double m_stiffness;
  
public:
  MassSpring (double m, double k)
    : m_mass(m), m_stiffness(k) {} 
  
  size_t dimX() const override { return 2; }
  size_t dimF() const override { return 2; }
  
  void evaluate (VectorView<double> x, VectorView<double> f) const override
  {
    f(0) = x(1);
    f(1) = -m_stiffness/m_mass * x(0);
  }
  
  void evaluateDeriv (VectorView<double> x, MatrixView<double> df) const override
  {
    df = 0.0;
    df(0,1) = 1;
    df(1,0) = -m_stiffness/m_mass;
  }
};

We can now use the TimerStepper for soling the ode. We create a NonlinearFunction object as MassSpring object, and pass it to the ExplicitEuler timer-stepper. Then we can run a simple time-loop to evolve the state by time-steps \(\tau\):

double tend = 4*M_PI;
int steps = 100;
double tau = tend/steps;

Vector<> y = { 1, 0 };  // initializer list
shared_ptr<NonlinearFunction> rhs = std::make_shared<MassSpring>(1, 1);
  
ExplicitEuler stepper(rhs);

std::cout << 0.0 << "  " << y(0) << " " << y(1) << std::endl;
for (int i = 0; i < steps; i++)
  {
     stepper.doStep(tau, y);
     std::cout << (i+1) * tau << "  " << y(0) << " " << y(1) << std::endl;
  }

This example is provided in demos/test_ode.cpp.

Using matplotlib from the a python script plotmassspring.py we generated the plots of the time evolution

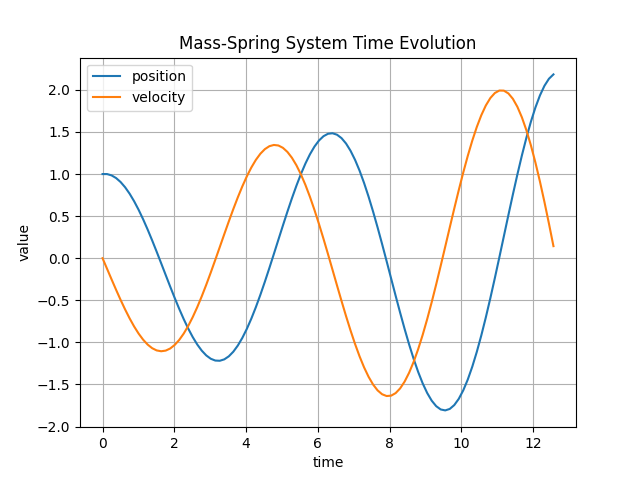
and the phase plot via plotting (position(t), velocity(t)) as a two dimensional curve:

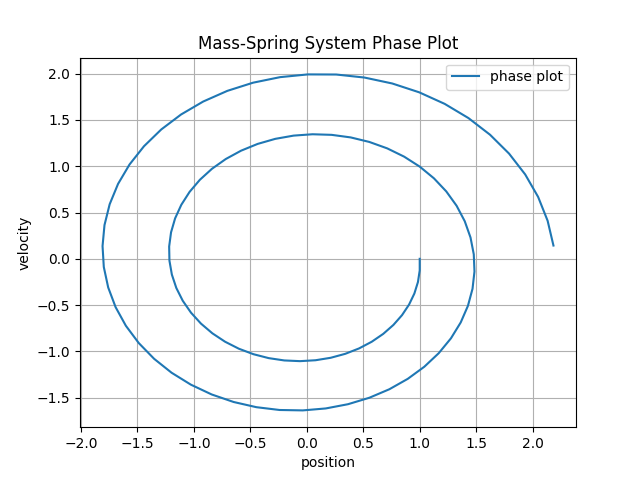
17.2.2. Exercise:

• build and run the explicit Euler method for the mass-spring system. Try with different time-steps and much larger end-times. Look at the time evolution and phase plots.

• Implement a ImprovedEuler time-stepping method defined as:

  \[\begin{eqnarray*} \tilde y & = & y_n + \tfrac{\tau}{2} f(y_n) \\ y_{n+1} & = & y_n + \tau f(\tilde y) \end{eqnarray*}\]

  Compare the obtained results with the explicit Euler method.

  Push your extensions to your github fork.