\[\begin{eqnarray*}
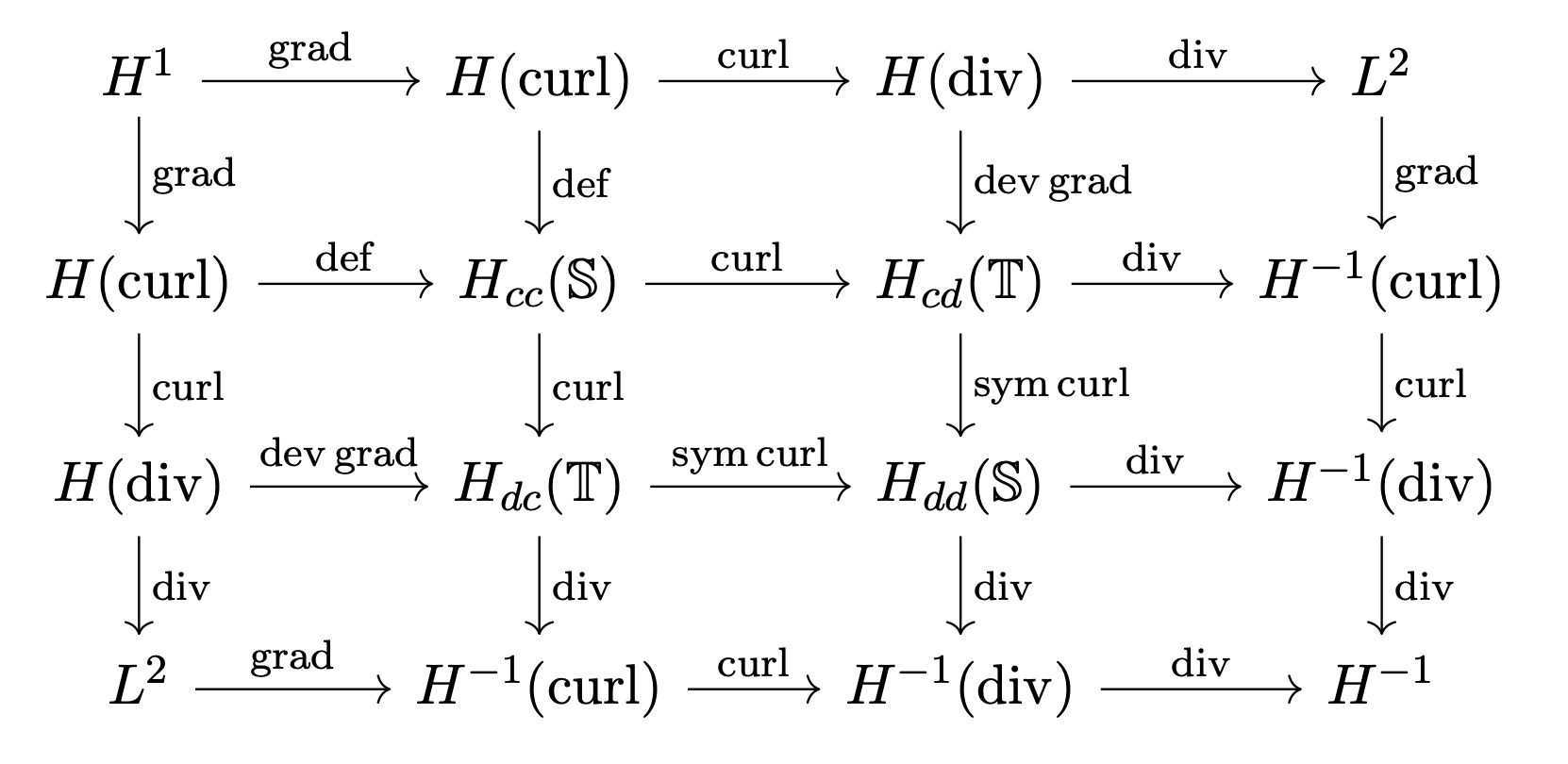
H(dd)
& := &
\{ \sigma \in L_2 (\mathbb{S})
: \operatorname{div} \operatorname{div} \, \sigma \in H^{-1}(\mathbb{R}) \} \\
H(cd) & := & \{ \sigma \in L_2(\mathbb{T})
: \operatorname{curl}
\operatorname{div} \sigma \in H^{-1}(\mathbb{V}) \} \\
H(cc) & := & \{ \sigma \in L_2(\mathbb{S}) : \operatorname{curl}^T
\operatorname{curl} \sigma \in H^{-1}(\mathbb{S}) \}
\end{eqnarray*}\]
\[\begin{eqnarray*}
V_{dd}^k & = & \{ \sigma \in L_2(\mathbb{S}) : {\sigma}_{|T} \in
P^k(\mathbb{S}), \sigma_{nn} \; \text{continuous} \} \\
V_{cd}^k & = & \{ \sigma \in L_2(\mathbb{T}) : {\sigma}_{|T} \in
P^k(\mathbb{T}), \sigma_{nt} \; \text{continuous} \} \\
V_{cc}^k & = & \{ \sigma \in L_2(\mathbb{S}) : {\sigma}_{|T} \in P^k(\mathbb{S}), \sigma_{tt} \; \text{continuous} \}
\end{eqnarray*}\]
Can be mapped from a reference-element with Piola / covariant transformations from the left and the right.
12.1. Applications:
TDNNS method for elasticity:
Find stress \(\sigma \in V_{dd}^k\) and displacement \(u \in {\mathcal N}^k\)
\[\begin{split}
\begin{array}{ccccll}
\int A \sigma : \tau & + & \left< \operatorname{div} \tau, u \right>
& = & 0 & \; \forall \, \tau \in V_{dd} \\[0.5em]
\left< \operatorname{div} \sigma, v \right> & & & = & f(v)
& \; \forall \, v \in {\mathcal N}
\end{array}
\end{split}\]
Astrid Pechstein (aka Sinwel) Phd-thesis and joint work [‘11,’12,’18,’21]
robust for thin structures.
MCS method for Stokes:
Find \(\sigma \in V_{cd}^k\), \(u \in {\mathcal BDM}^k\), and \(p \in
P^{k-1}\):
\[\begin{split}
\begin{array}{ccccll}
\int A \sigma : \tau & + & \left< \operatorname{div} \tau,
u \right> + (\operatorname{div}
u, q)
& = & 0 & \; \forall \, \tau \in V_{cd}, \, \forall \, q \in P^{k-1} \\[0.5em]
\left< \operatorname{div} \sigma, v \right> +(\operatorname{div} v,p) & & & = & f(v)
& \; \forall \, v \in {\mathcal BDM}^k
\end{array}
\end{split}\]
Philip Lederer Phd-thesis, P. Lederer-J. Gopalakrishnan-JS [‘20, ‘20]
exact divergence free discrete velocities, pressure-robust
Hellan-Herrmann-Johnson (HHJ) method for the Kirchhoff plate:
[’60s and ’70s, Arnold+Brezzi ‘85, I. Comodi ‘89]
Find bending moments \(\sigma \in V_{dd}^k\) and vertical deflection \(w \in {\mathcal L}^{k+1}\):
\[\begin{split}
\begin{array}{ccccll}
\int A \sigma : \tau & + & \left< \operatorname{div} \tau, \nabla w \right>
& = & 0 & \; \forall \, \tau \in V_{dd}^k \\[0.5em]
\left< \operatorname{div} \sigma, \nabla v \right> & & & = & f(v)
& \; \forall \, v \in {\mathcal L}^{k+1}
\end{array}
\end{split}\]
Combination of HHJ and TDNNS for Reissner Mindlin
[A. Pechstein-JS ‘17]:
Find \(\sigma \in V_{dd}^k\) and \(w \in {\mathcal L}^{k+1}\), \(\beta \in {\mathcal N}^{k}\):
\[\begin{split}
\begin{array}{ccccll}
\int A \sigma : \tau & + & \left< \operatorname{div} \tau, \beta \right>
& = & 0 & \; \forall \, \tau \in V_{dd}^k \\[0.5em]
\left< \operatorname{div} \sigma, \delta \right> & -
& \tfrac{1}{t^2} (\nabla w
- \beta, \nabla v - \delta) & = & f(v)
& \; \forall \, v \in {\mathcal L}^{k+1}, \; \forall \, \delta \in {\mathcal N}^k,
\end{array}
\end{split}\]
Free of locking, and for \(t \rightarrow 0\) the discrete RM solution
converges to the Kirchhoff solution.