NGSolve Model Templates:

A python library on top of NGSolve providing state of the art numerical methods for many equations.

Navier Stokes

hybrid mixed method for Navier-Stokes (Gopalakrishnan+Lederer+Schöberl ‘20,’20), Dissertation Lederer 2019

from ngsolve import *
import netgen.geom2d
import netgen.meshing
from ngsolve.webgui import Draw

from ngs_templates.NavierStokes import *
ngsglobals.msg_level = 0

Geometry and mesh:

geo = netgen.geom2d.SplineGeometry()
geo.AddRectangle( (0, 0), (2, 0.41), bcs = ("wall", "outlet", "wall", "inlet"))
geo.AddCircle ( (0.2, 0.2), r=0.05, leftdomain=0, rightdomain=1, bc="cyl", maxh=0.02)
mesh = Mesh( geo.GenerateMesh(maxh=0.07))
Draw (mesh)
mesh.Curve(3);

timestep = 0.001
navstokes = NavierStokes (mesh, nu=0.001, order=4, timestep = timestep,
                              inflow="inlet", outflow="outlet", wall="wall|cyl",
                              uin=CoefficientFunction( (1.5*4*y*(0.41-y)/(0.41*0.41), 0) ))
                              

navstokes.SolveInitial()

scene = Draw (Norm(navstokes.velocity), mesh, "velocity")

tend = 5
t = 0
cnt = 0
with TaskManager():
    while t < tend:
        navstokes.DoTimeStep()
        t = t+timestep
        cnt = cnt+1
        if cnt % 100 == 0:
            print ("t = ", t, "  ", end='\r')
            scene.Redraw()

t =  0.10000000000000007   
t =  0.20000000000000015   
t =  0.3000000000000002   

t =  0.4000000000000003   
t =  0.5000000000000003   
t =  0.6000000000000004   

t =  0.7000000000000005   
t =  0.8000000000000006   
t =  0.9000000000000007   

t =  1.0000000000000007   
t =  1.0999999999999897   
t =  1.1999999999999786   

t =  1.2999999999999676   
t =  1.3999999999999566   
t =  1.4999999999999456   

t =  1.5999999999999346   
t =  1.6999999999999236   
t =  1.7999999999999126   

t =  1.8999999999999015   
t =  1.9999999999998905   
t =  2.0999999999998797   

t =  2.1999999999998687   
t =  2.2999999999998577   
t =  2.3999999999998467   

t =  2.4999999999998357   
t =  2.5999999999998247   
t =  2.6999999999998137   

t =  2.7999999999998026   
t =  2.8999999999997916   
t =  2.9999999999997806   

t =  3.0999999999997696   
t =  3.1999999999997586   
t =  3.2999999999997476   

t =  3.3999999999997366   
t =  3.4999999999997256   
t =  3.5999999999997145   

t =  3.6999999999997035   
t =  3.7999999999996925   
t =  3.8999999999996815   

t =  3.9999999999996705   
t =  4.099999999999704   
t =  4.199999999999737   

t =  4.299999999999771   
t =  4.399999999999804   
t =  4.4999999999998375   

t =  4.599999999999871   
t =  4.699999999999904   
t =  4.799999999999938   

t =  4.899999999999971   
t =  5.000000000000004   

The code for the MCS - Navier-Stokes solver

• mixed method with \(u_h \in BDM^k \subset H(div)\)

• upwind DG for convetive term

• uses SIMPLE time-stepping

• hybrid mixed system for pressure correction

see NGSolve/modeltemplates

Our first flying plane (by Philip Lederer)

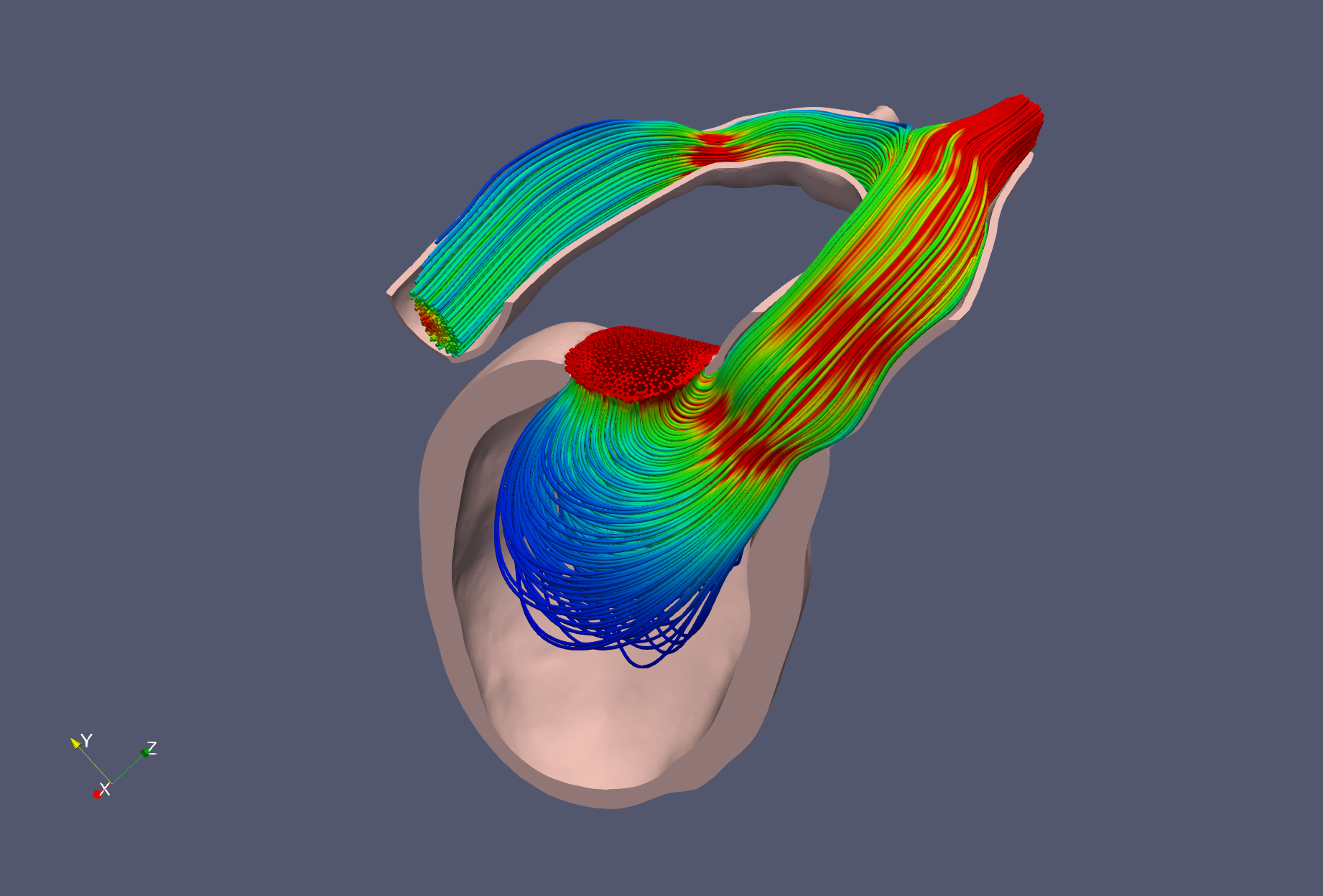
heart model simulation using MCS